はじめに
こんにちは。dely開発部の辻です。
本記事はdely Advent Calendar 2019の4日目の記事です。
昨日は弊社CXO坪田が「突破するプロダクトマネジメント」という記事を書きました!
プロダクトマネージメントっていつの時代も課題山積ですよね。弊社も多分に漏れずたくさんの課題を抱えているわけですが、それらをどのように突破していくか様々な観点からの具体的な取り組みが書かれていますので興味のある方は是非読んでみてください。南無。

さて本日は「Jupyterもいいけど、SageMath使って可能性もっと伸ばそう!」ということで、普段Jupyter Notebook使ってるという人向けに、どうせならSageMathを使ってやれること増やしませんか?という内容になっています。そこで、SageMathのインストールから基本的な使い方、趣味(?)や実務で普段どんなふうに活用しているかなどご紹介させてもらおうと思います。
目次
SageMathとは

SageMath(元々は単にSageという名前でした)は、主に数学に関するなんやかんやの処理が非常に便利に使えるというツールです。Pythonで書かれているためPythonでできることはもちろんできますし、Jupyter Notebook上でカーネルとして利用することもできます。同様の数式処理システムにMaximaというLISPで書かれたものがあるのですが、これはSageMathに同梱されていますので、個人的にはそちらもよく使います。
SageMath - Open-Source Mathematical Software System
Maxima, a Computer Algebra System
SageMathのインストール
SageMathをMacにインストールするときには、上のリンクから「sage-8.9-OSX_10.14.6-x86_64.dmg」(2019.12.04時点)をクリックしてダウンロードして、お使いのシェルの設定ファイルにこんな(↓)エイリアスを書いてあげればOKです。最新バージョンは8.9です。
alias sage='/Applications/SageMath/sage'
これで、ターミナルでSageMathが利用できるようになります。
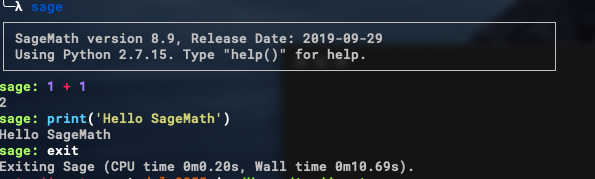
または、ターミナルで以下のコマンドを実行するとJupyter notebookが開きます。
sage -n jupyter
カーネルSage8.9でノートを開くと見慣れた形で表示されます。
あるいは、このように notebook() と入力すると、The Sage Notebook が開きます。
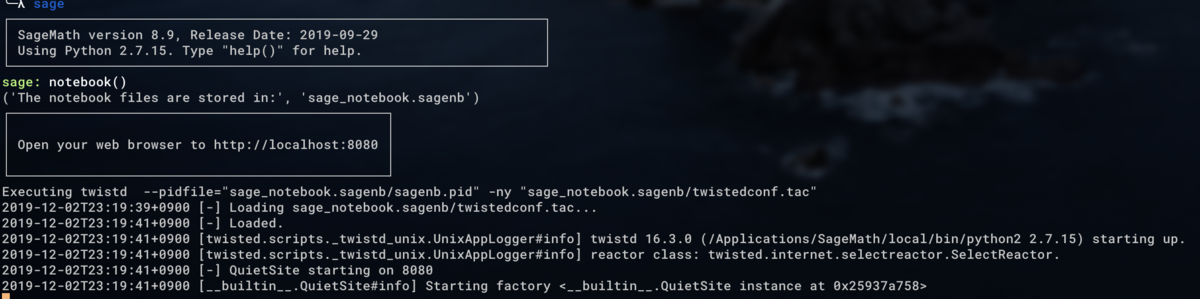
見た目がちょっと違いますが使い方はほとんど同じです。
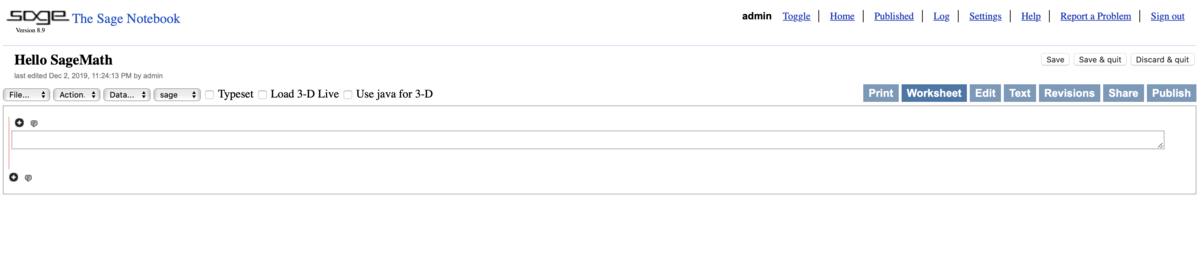
ここで最初にお伝えしておきたいのが、SageMathは結構デカいということです。なので、ローカル環境にインストールするとまあまあ容量を食います。それが嫌という方はオンラインでの利用をおすすめします。ちょっと試してみたいという場合は、こちら(↓)の「Sage Cell Server」がおすすめです。
Sage Cell Serverを使うと小窓にコードを書いてEvaluateボタンを押すだけでSageMathのBuilt-in関数などがそのまま利用できてとても便利です。SageMathのサンプル集からコピペするだけで、こんな感じのシェルピンスキーのギャスケットが簡単に描けます。
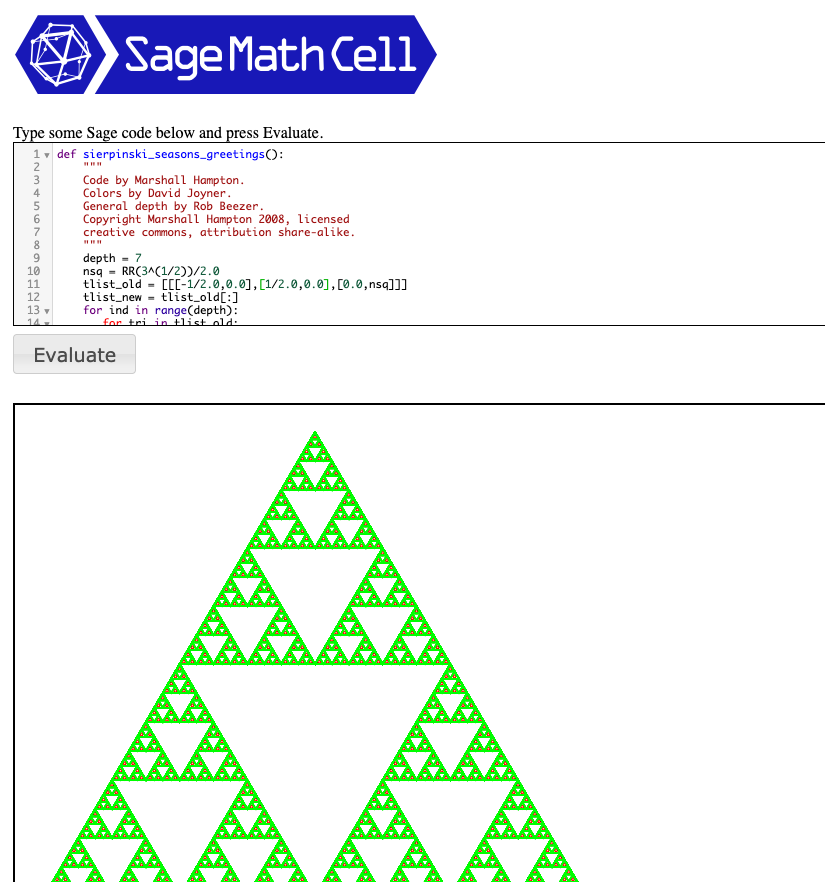
あるいは、もっとちゃんと使いたいという方にはこちらの「CoCalc」というサービスがおすすめです。
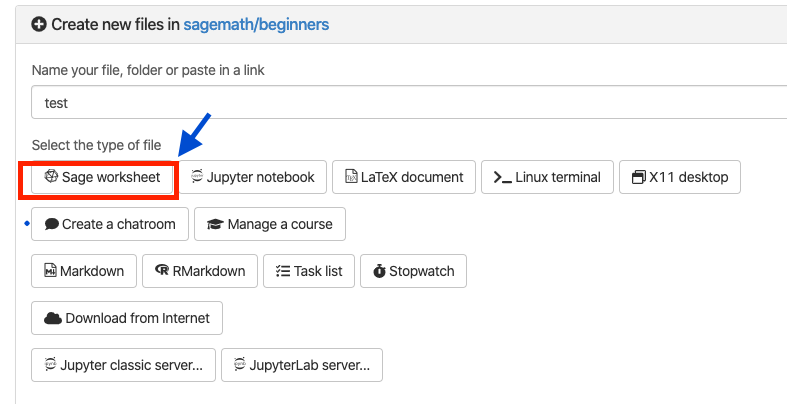
こちらの「Sage worksheet」を選択してワークシートを作成すると、「.sagews」という拡張子のファイルが作成されます。見た目はちょっと違うんですが、操作方法などはJupyter Notebookとほとんど同じですので、使い勝手はいいと思います。少し使うだけなら無料で問題ないと思うのですが、使う頻度が多くなってメモリやCPU数を増やしたいという場合には有料となりますのでご注意ください。
SageMakerでSageMathを使いたい!
SageMakerとSageMath、とても似た名前ですが全くの別物です。SageMakerはAWSが提供する機械学習サービスで、すべての開発者とデータサイエンティストに機械学習モデルの構築、トレーニング、デプロイ手段を提供するために生まれたサービスです。SageMakerではJupyter NotebookをVMインスタンスとして立ち上げることが可能なので、このノートブックインスタンスにSageMathを入れて普段から使っていきたいと思います。

さっそくノートブックインスタンスを立ち上げます。

ノートブックインスタンスのJupyter Notebookを開いてPython2をアクティベートします。

SageMathは基本Python2で動きます。Python3については以下のSageMath FAQで以下のような言及がありますので、実験的ではありますが利用は可能のようです。(個人的には実験していないのでぜひチャレンジした結果を教えていただきたいです。)
As of August 2019, most of SageMath works fine with Python 3. However, we still consider Python 3 support to be experimental and no official Python 3 release has been made yet. You can build the source code of SageMath with Python 3 using the instructions at the bottom of https://wiki.sagemath.org/Python3-compatible%20code See trac ticket #15530 and trac ticket #26212 for tracking the current progress.
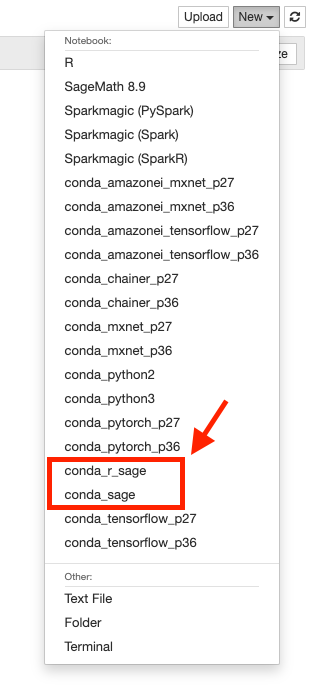
ここで、 こちらのSageMathの公式にしたがってconda経由でインストールしていきます。
Install from conda-forge — Sage Installation Guide v9.0
conda install mamba -c conda-forge mamba create -n sage sage -c conda-forge
そうすると、このようにターミナル上でsageコマンドが利用できるようになります。
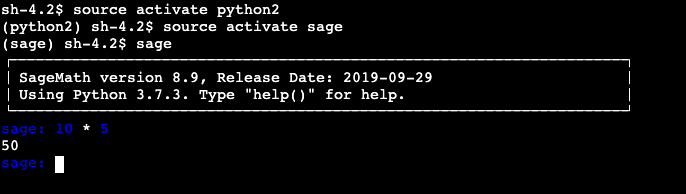
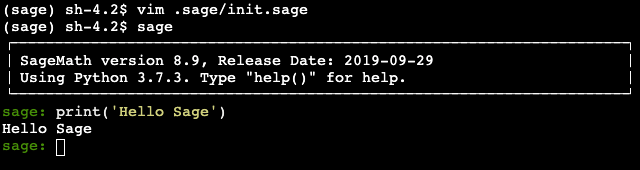
しかし、そのままだと sage の文字が濃い青色でとても見づらいので、$HOME/.sage/init.sage ファイルを作成して以下の1行を追加してあげると見やすくていい感じになります。
%colors Linux
こんな感じです。
これらの設定を毎回インスタンス起動のたびにやるのはとても面倒ですので、SageMakerにはライフサイクル設定という仕組みがあります。そちらにここまでのコマンドを追記することで、インスタンス起動時にSageMathが使える状態にすることが可能です。詳しくは(↓)こちら。
https://docs.aws.amazon.com/ja_jp/sagemaker/latest/dg/notebook-lifecycle-config.html
また、このようにSageMathの環境が利用できるカーネルに追加されます。
ちなみに、iPadを利用している方向けの話になってしまいますが、Junoというアプリを使って、SageMakerのノートブックインスタンスやCoCalcと連携させることが可能です。そうすると、自分の描いた3Dグラフを直接指で触って回転したりできるのでとても面白いです。
iPad上で描いたグラフを指で回わしているところ
有料ですが個人的にはとても重宝しています。
apps.apple.comSageMathを使ってみよう
それでは、ここから先はSageMathを実際に使っていきたいと思います。基本的にはPythonと同じように利用することができるので、SageMathを利用されたことがない人もすぐに慣れると思います。
基本操作
チュートリアル的なことをしてもあまり面白くないので、その辺りはこちらのSage観光ツアーをご参照ください。
せっかくなので、この中から少し例としてサンプルを紹介してみたいと思います。
まずは、こちらの単純な2次方程式の解を解析的に求めたい場合を考えます。
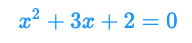
こちらの方程式の解をSageMathを使って求めるとこのよう(↓)になります。
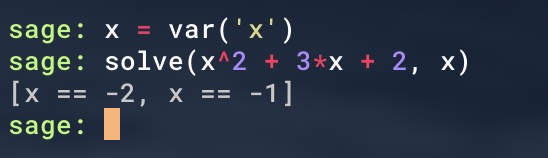
変数xを定義して、解きたい方程式と変数をsolve関数の引数に入れるだけです。めちゃくちゃ簡単ですね。 一応念のため、こちらを関数としてグラフを描くとこのように(↓)なるので、まあ蛇足ですがこの解で合ってそうです。
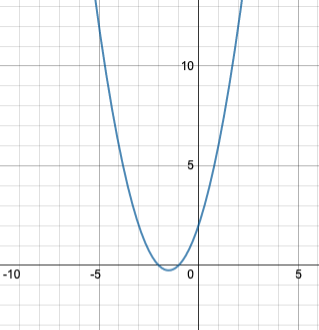
それではもう一つ、機械学習などではたびたび登場する偏微分のかんたんな例を紹介してみようと思います。 こちらの関数をxとyそれぞれについて偏微分したい場合を考えます。
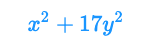
流れは先ほどの例と同様で、変数x,yを定義して、偏微分対象の関数を定義します。微分関数であるdiff関数の引数として偏微分対象の変数を入れるだけ、です。 こちらも非常にかんたんですね。
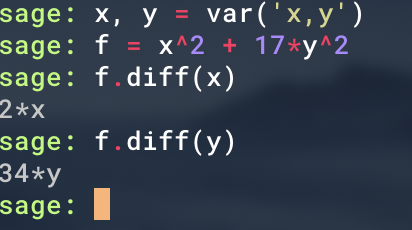
楕円曲線で遊んでみる
さて、ここからはちょっと素人なりに頑張って楕円曲線で遊んでみたいと思います。ここまでの例だけですと、なんだScipyあればできるじゃんという話ですが、楕円曲線j-不変量の計算などを行う際にはSageMathの力を使うととても楽チンになります。ちなみに楕円曲線は暗号化アルゴリズムでおなじみ(量子超越性によって暗号が破られる日は来るのか?!)ですが、厳密には種数 1 の非特異な射影代数曲線、さらに一般的には、特定の基点 O を持つ種数 1 の代数曲線のことをいいます。では早速、以下のヴァイエルシュトラス方程式が与えられていると仮定したときに無限遠点を群演算における零元であるとして話を進めていきましょう。
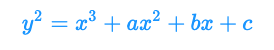
まず、手始めに具体的な係数を当てはめて適当な楕円曲線を作ってみます。
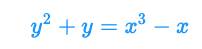
この楕円曲線をSageMathではこのように(↓)表現します。(ここからはCoCalcを使っていきます。)
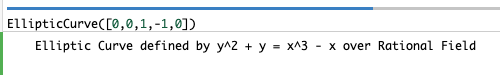
EllipticCurveコンストラクタの引数は、EllipticCurve([a1, a2, a3, a4, a6 ])と以下の係数が対応しています。(対応する順序が訳のわからないことになっているので注意してください。)
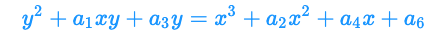
j-不変量 j = 1 を持つ楕円曲線を生成したい場合は、このように(↓)表現します。
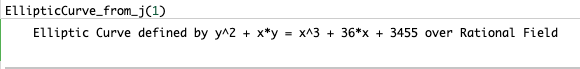
このことから、j-不変量 1 の楕円曲線が以下のような式(↓)になることがわかります。楽しいですね。
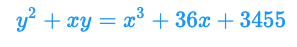
それではここから、以下の代表的な楕円曲線についてSageMathを使っていろいろと遊んでいくことにしましょう。
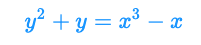
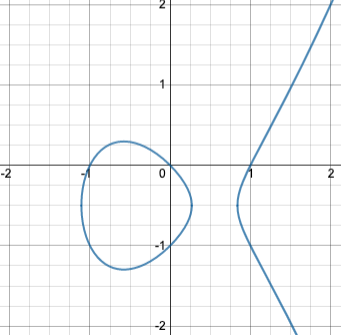
この楕円曲線のグラフを描くと、このように点(0,0)を通りつながった円の形状と、右にハの字に広がった形状とがある、いわゆるよくみる楕円曲線の形になっています。
さて、それではSageMathを使ってこの楕円曲線の持つ加法群構造を調べていきたいと思います。
まずはこのように(↓)対象の楕円曲線を生成します。
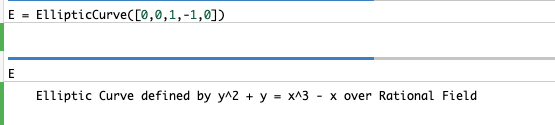
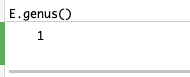
一応念のため、ちゃんと種数1の非特異曲線になっているか確認してみます。
数式を確認したい場合はwebブラウザ上で数式を明瞭に表示するためMathJaxをimportしてインターフェースを利用します。

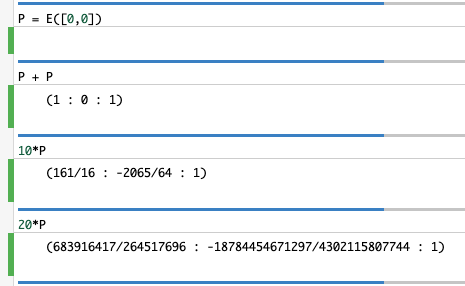
有理点(0,0)について、無限遠点が零元、同一曲線上の3点を加えると0となる加法群の構造を備えているか調べます。 確かに計算してみると、3点加えると0で、倍数も一見訳のわからない有理数ではありますが、ちゃんと同一曲線上で有理点になっていることが確認できます。
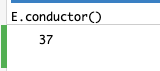
導手の数もこのように簡単に表せます。
最後に、この楕円曲線に随伴するL-級数、あるいはモジュラー形式の係数、あと階数をSageMathを計算してみます。あっという間です、膨大な手計算されていた頃の偉大なる数学者たちに対して申し訳ないほどの簡単さです。

こちらの例では30ですが、係数を10000以下すべてとした場合でも、計算するのにかかる時間はたったの約1秒ほどです。非常に高速に計算することができます。
ちょっとだけMaximaの紹介
冒頭で、ちょっとだけ触れましたがMaximaという数式処理システムがありまして、そちらはLISP言語の実装なのですがインターフェースがSageMathに同梱されているのでそのまま使うことができます。実はMaximaを単体でインストールして使う場合はgnuplotなどの設定が少々癖があって面倒なのですが、同梱されているのでサクッと使えて便利です。
たとえばこちらの1行で何が表示されるかといいますと。。
maxima.plot3d("[cos(x)*(3 + y*cos(x/2)), sin(x)*(3 + y*cos(x/2)), y*sin(x/2)]","[x, -4, 4]", "[y, -4, 4]", '[plot_format, openmath]')
このように「メビウスの帯」がXmaximaに表示されます。
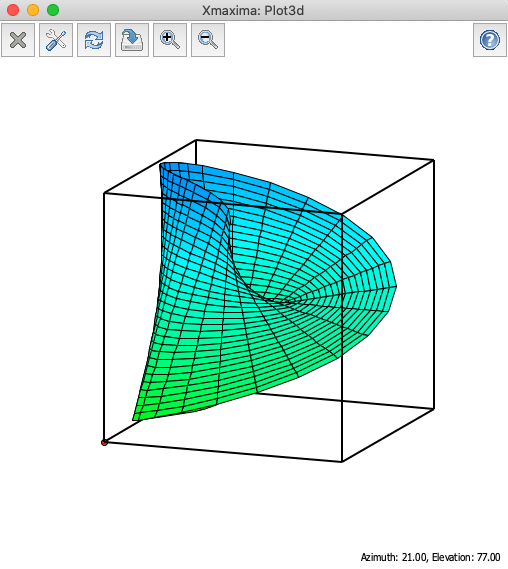
Xmaximaはマウスでグルグル動かすことができるので先ほどのJunoがなくても手軽にグラフの形状を確認できて便利です。
ルービックキューブ群
SageMathに同梱されているインターフェースといえば、ちょっと変わり種のものとしてルービックキューブ群があります。 こういう感じでキューブの展開図を表示できます。
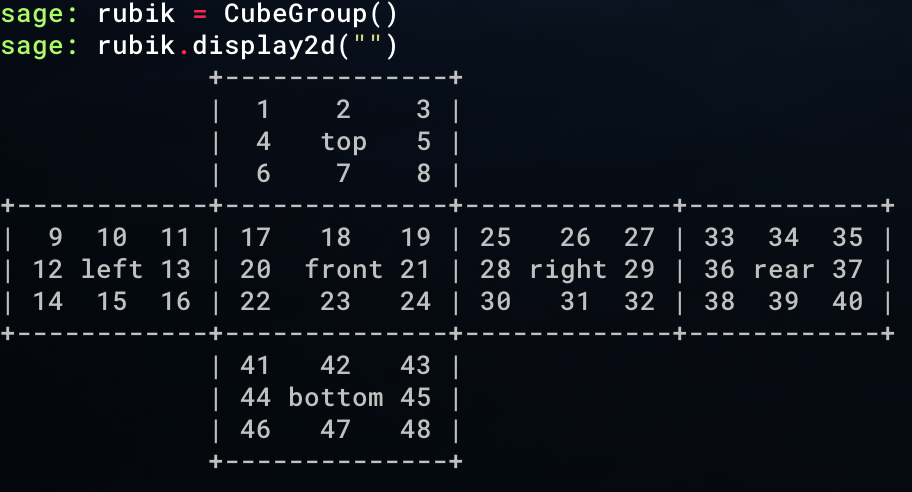
あるキューブの状態のときの解法を出力してくれて、その解が正しいかも確認できます。

実務で使いどころ
さて、冒頭でご紹介した通り、SageMathは数学に関するなんやかんやの処理が非常に便利に使えるという点については、ここまで一通り使い方をみていただいて「ふむふむ、なるほど」とご理解いただけたものとして、では実際の業務にどのように応用していくのかという点がやっぱり気になると思います。
それについて結論からお伝えしますと、現時点では、分析や最適化問題のシミュレーションがメインです。とはいえ別にプロダクションコードには使えないというわけではないんですが、やっぱりSageMathがライブラリとしてサイズがデカすぎるのでポータビリティが非常に低いという点がネックになります。(デプロイも大変ですしね。)
ただ、いずれもしかしたら、今後どこかのタイミングで楕円曲線やTDA(topological data analysis)など活用する機会がでてくるようなことがあれば、SageMathを利用したプロダクションコードが生まれる可能性もなくはないと個人的にはとても期待しています。ですので、まあ今はその準備段階と捉えて必要に応じて適度に利用しているといったところです。
それを踏まえまして、よく実務で登場する最適化問題の例としてナップザック問題と、機械学習ではおなじみの最尤推定でよく使うEMアルゴリズムについてご紹介しましょう。

まず、ナップザック問題ですが、自分で実装するとなるとまあまあめんどくさいと感じている方は多いのではないでしょうか?(最終的には制約が多くなってしまうので、実装が複雑になるのは当然だとしても、少なくとも導入当初はサクッと評価したいですよね。)実はSageMathにはknapsack関数があらかじめ用意されています。 たとえばこんな問題があるとします。
問題
4つの商品(重さ、価値)で定義される項目が、 それぞれA(100g, 200円)、B(150g, 100円)、C(50g, 300円)、 D(70g, 250円)でした。 バッグの最大重量200gのとき、価格を最大にして詰められる組み合わせはどれか?
これはつまり、福袋はある程度軽くて価値が高いものがいっぱい入ってると嬉しいといった趣旨の問題ですね。
SageMathを使えば、このように(↓)knapsack関数をimportしてそれぞれの条件の組みを引数に渡すだけで、はい終わりです。

一見、100gの商品Aを入れた方が高額になりそうな気もしますが、実はCとDを詰めたほうが全体では高額になるということがわかりました。
続きまして、EMアルゴリズムも一から実装するとなるとそれなりに骨が折れると思います。この場合もSageMathのBuilt-in関数を使って気楽に実装することができます。 今回はPRMLの例からよくある混合ガウス分布のEMアルゴリズムについてSageMathで実装するケースをご紹介させていただきます。EMアルゴリズム自体の説明は割愛させていただきますが、レコメンドでの利用だけでなく混合ガウス分布は割と実務のEDAでも頻繁に登場しますのでEMアルゴリズムを活用する場面はその点でも多いかと思います。
なお、こちらの例では平均初期値を(−1.5, 0.5) , (1.5, −0.5)とし、分散初期値を0.5として計算した場合となっています。
まず、全体として以下のような(↓)関数呼び出しを考えます。
pi_k = [0.5, 0.5] mu_k = [vector([-1.5, 0.5]), vector([1.5, -0.5])] sigma_k = [matrix(RDF, D, D, beta*ident), matrix(RDF, D, D, beta*ident)] EM(pi_k, mu_k, sigma_k)
そしてこちらが(↓)EM()の実装です。これは基本的にEMアルゴリズムをそのまま実装したものになります。
def EM(pi_k, mu_k, sigma_k): diff = 1 for l in range(21): pi_N = matrix(RDF, [[pi_k[k] * _gauss(X[n], mu_k[k], sigma_k[k]) for k in range(K)] for n in range(N)]) o_lnP = ln_p() gamma = matrix(RDF, N, K) for n in range(N): gamma.set_row(n, pi_N[n]/(pi_N[n].sum())) # Eステップ if l == 0: action_f(mu_k, sigma_k, gamma) # Mステップ N_k = [gamma.column(k).sum() for k in range(K)] for k in range(K): mu_k[k] = 0 for n in range(N): mu_k[k] += gamma[n][k]*X[n] mu_k[k] /= N_k[k] sigma_k[k] = 0 for n in range(N): sigma_k[k] = sigma_k[k] + gamma[n][k]*covMatrix(X[n], mu_k[k]) sigma_k[k] /= N_k[k] pi_k[k] = N_k[k]/N lnP = ln_p() diff = abs(lnP - o_lnP) o_lnP = lnP # print if action_idx.has_key(l): action_f(mu_k, sigma_k, gamma)
x, yは混合ガウス分布に従ったデータであるものとして、各種定数の初期化を行います。
# x, y は混合ガウス分布 # 定数の初期化 D = 2 K = 2 N = len(x) beta = 0.5 X = matrix(RDF, zip(x, y)) ident = identity_matrix(2) # アクションのインデックス action_idx = {0:0, 1:1, 5:5, 20:20}
最後に、EM()関数から呼び出される必要な関数を定義します。
def _gauss(v, mu, sigma): d = len(v); sigma_inv = sigma.inverse(); sigma_abs_sqrt = sigma.det().sqrt(); val = -(v - mu) * sigma_inv * (v - mu).column()/2; a = (2*pi)**(-d/2) * sigma_abs_sqrt**-0.5 return a * e**val[0]; def covMatrix(x, u): d = x - u return matrix(RDF, [[d[i]*d[j] for j in range(D)] for i in range(D)]) def ln_p(): sum = 0.0 for n in range(N): sum += ln(pi_N[n].sum()) return sum def action_f(mu_k, sigma_k, gamma): pt_plt = Graphics() for n in range(N): pt_plt += point(X[n], rgbcolor=(gamma[n][1], 0, gamma[n][0])) r_cnt_plt = contour_plot(lambda x, y : _gauss(vector([x, y]), mu_k[1], sigma_k[1]), [x, -2.5, 2.5], [y, -2.5, 2.5], contours = 1, cmap=['red'], fill=False) b_cnt_plt = contour_plot(lambda x, y : _gauss(vector([x, y]), mu_k[0], sigma_k[0]), [x, -2.5, 2.5], [y, -2.5, 2.5], contours = 1, cmap=['blue'], fill=False) (r_cnt_plt + b_cnt_plt + pt_plt).show(aspect_ratio=1, figsize=(3), xmin=-2.5, xmax=2.5, ymin=-2.5, ymax=2.5)
まとめ
いかがでしたでしょうか?
本日は、Jupyter Notebookもいいんだけど、それプラスアルファのことができるSageMathをぜひ使ってみてはいかがでしょうというご紹介をさせていただきました。SageMathって何?というところから出発して、インストール方法やコマンドでの利用やオンラインでの利用についてご紹介した後、ほんの一部ですがSageMathの簡単な使い方などご紹介をさせていただきました。こんな便利なツールが無料であるなんて今の時代は本当に恵まれていますね、ぼくが学生時代にSageMath欲しかったなぁと心底思います。
参考
Sage チュートリアル http://doc.sagemath.org/pdf/ja/tutorial/tutorial-jp.pdf

- 作者:J. H. シルヴァーマン,J. テイト
- 出版社/メーカー: 丸善出版
- 発売日: 2012/08/25
- メディア: 単行本

- 作者:C.M. ビショップ
- 出版社/メーカー: 丸善出版
- 発売日: 2012/04/05
- メディア: 単行本(ソフトカバー)

- 作者:C.M. ビショップ
- 出版社/メーカー: 丸善出版
- 発売日: 2012/02/29
- メディア: 単行本
さいごに
さて次回は、サーバサイドエンジニアの安尾が「スピード優先の開発で溜まった技術的負債の返済計画(サーバーサイド編)」というタイトルで投稿します!
お楽しみに!
ちなみに
delyの開発チームについて詳しく知りたい方はこちらもあわせてどうぞ!
CXOとVPoEへのインタビュー記事はこちら!

